3. Tidal simulation in the Orkney island¶
3.1. Introduction¶
This example demonstrates how OpenTidalFarm can be used for simulating the tides in a realistic domain.
- It shows how to:
load a mesh from file;
use realistic tidal forcing on the open boundaries;
load the bathymetry from a NetCDF file;
use a non-homogenous viscosity;
solve a time-dependent shallow water solver and store the results to file.
We will be simulating the tides in the Pentland Firth, Scotland for 12.5 hours, starting at 14:40 am on the 18.9.2001. The flow result at the end of the simulation looks like:
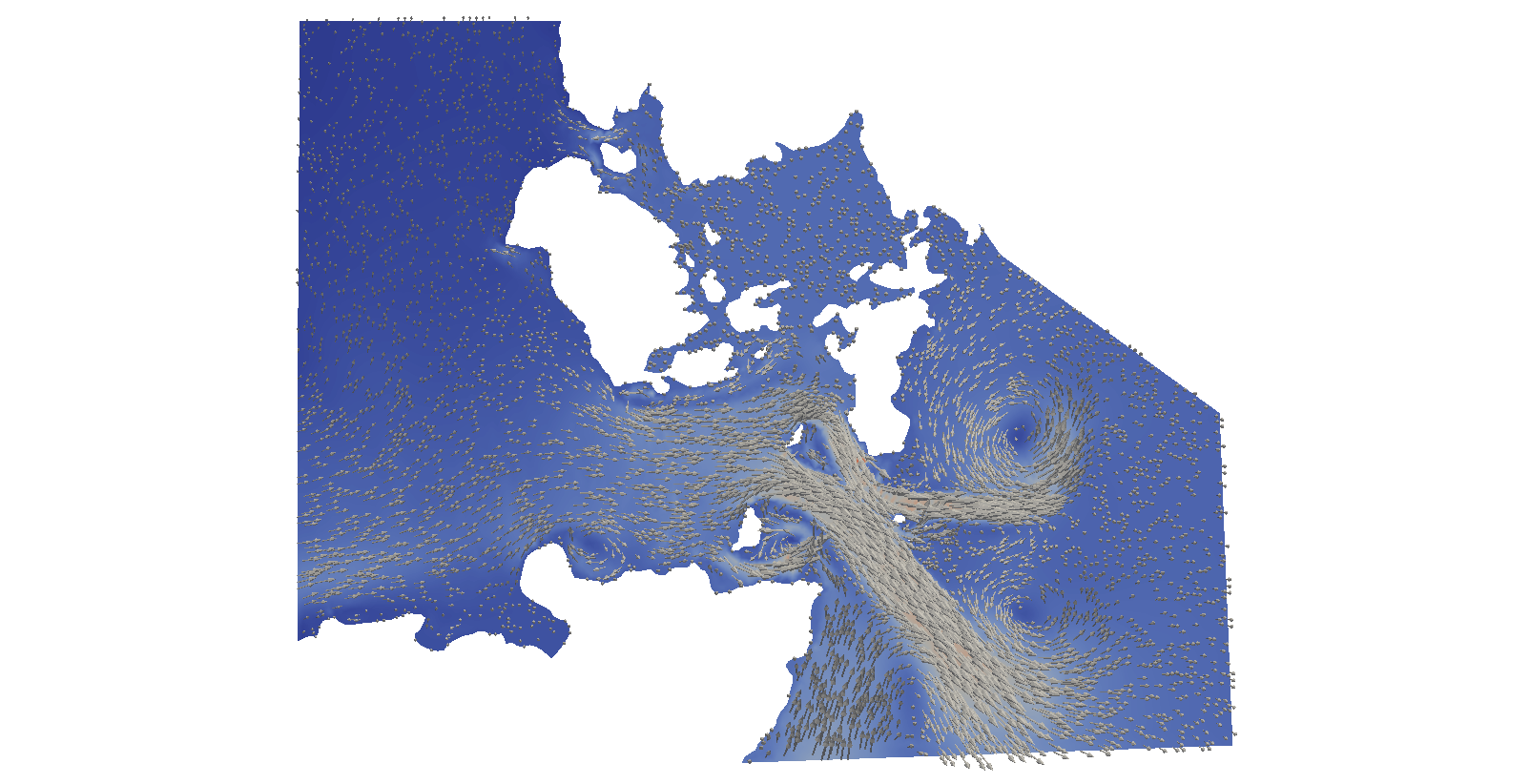
This example requires some large data files, that must be downloaded separately by calling in the source code directory:
git submodule init
git submodule update
3.2. Implementation¶
We begin with importing the OpenTidalFarm module.
from opentidalfarm import *
set_log_level(ERROR)
We also need the datetime module for the tidal forcing.
import datetime
Next we define the UTM zone and band, as we we will need it multiple times later on.
utm_zone = 30
utm_band = 'V'
Next we create shallow water problem and attach the domain and boundary conditions
prob_params = SWProblem.default_parameters()
We load the mesh in UTM coordinates, and boundary ids from file
domain = FileDomain("../data/meshes/orkney/orkney_utm.xml")
prob_params.domain = domain
The mesh and boundary ids can be visualised with
#plot(domain.facet_ids, interactive=True)
Next we specify boundary conditions. We apply tidal boundary forcing, by using
the TidalForcing class.
eta_expr = TidalForcing(grid_file_name='../data/netcdf/gridES2008.nc',
data_file_name='../data/netcdf/hf.ES2008.nc',
ranges=((-4.0,0.0), (58.0,61.0)),
utm_zone=utm_zone,
utm_band=utm_band,
initial_time=datetime.datetime(2001, 9, 18, 10, 40),
constituents=['Q1', 'O1', 'P1', 'K1', 'N2', 'M2', 'S2', 'K2'], degree=2)
bcs = BoundaryConditionSet()
bcs.add_bc("eta", eta_expr, facet_id=1)
bcs.add_bc("eta", eta_expr, facet_id=2)
# Apply a strong no-slip boundary condition. This can be changed to
# free slip (weakly enforced), by leaving out the Constant((0, 0))
# argument and changing bctype to "free_slip"
bcs.add_bc("u", Constant((0, 0)), facet_id=3, bctype="strong_dirichlet")
prob_params.bcs = bcs
Next we load the bathymetry from the NetCDF file.
bathy_expr = BathymetryDepthExpression(filename='../data/netcdf/bathymetry.nc',
utm_zone=utm_zone, utm_band=utm_band, domain=domain.mesh, degree=2)
prob_params.depth = bathy_expr
The bathymetry can be visualised with
#plot(bathy_expr, mesh=domain.mesh, title="Bathymetry", interactive=True)
Equation settings
For stability reasons, we want to increase the viscosity at the inflow and
outflow boundary conditions. For that, we read in a precomputed function
(generated by `compute_distance`) and
V = FunctionSpace(domain.mesh, "CG", 1)
dist = Function(V)
File("dist.xml") >> dist
With that we can define an expression that evaluates to a nu_inside value inside the domain and a nu_outside value near the in/outflow boundary.
class ViscosityExpression(Expression):
def __init__(self, *args, **kwargs):
self.dist_function = kwargs["dist_function"]
self.nu_inside = kwargs["nu_inside"]
self.nu_boundary = kwargs["nu_boundary"]
self.dist_threshold = kwargs["dist_threshold"]
def eval(self, value, x):
if self.dist_function(x) > self.dist_threshold:
value[0] = self.nu_inside
else:
value[0] = self.nu_boundary
Finally, we interpolate this expression to a piecewise discontinuous, constant function and attach it as the viscosity value to the shallow water problem.
W = FunctionSpace(domain.mesh, "DG", 0)
nu = ViscosityExpression(dist_function=dist, dist_threshold=1000, nu_inside=10., nu_boundary=1e3, degree=1)
nu_func = interpolate(nu, W)
prob_params.viscosity = nu_func
The other parameters are set as usual.
prob_params.friction = Constant(0.0025)
# Temporal settings
prob_params.start_time = Constant(0)
prob_params.finish_time = Constant(12.5*60*60)
prob_params.dt = Constant(5*60)
# The initial condition consists of three components: u_x, u_y and eta.
# Note that we set the velocity components to a small positive number, as some
# components of the Jacobian of the quadratic friction term is
# non-differentiable.
prob_params.initial_condition = Constant((DOLFIN_EPS, DOLFIN_EPS, 1))
# Now we can create the shallow water problem
problem = SWProblem(prob_params)
# Next we create a shallow water solver. Here we choose to solve the shallow
# water equations in its fully coupled form:
sol_params = CoupledSWSolver.default_parameters()
solver = CoupledSWSolver(problem, sol_params)
Now we are ready to solve and save the results to file.
f_u = XDMFFile("results/u.xdmf")
f_eta = XDMFFile("results/eta.xdmf")
# To save memory, we deactivate the adjoint model with annotate=False.
# We do not need the adjoint because we will not solve an optimisation problem
# or compute sensitivities
for sol in solver.solve(): #annotate=False):
print "Computed solution at time {}.".format(sol["time"])
# Write velocity and free-surface perturbation to file.
f_u.write(sol["u"], sol["time"])
f_eta.write(sol["eta"], sol["time"])
3.3. How to run the example¶
The code for this example can be found in examples/tidal-simulation/ in the
OpenTidalFarm source tree, and executed as follows:
$ mpirun -n 4 python orkney-coupled.py
where 4 should be replaced by the number of CPU cores available.
The results are stoed in the results directory and can be visualised with Paraview.