5. Farm layout optimization¶
This demo optimizes the position of 32 turbines in a tidal farm within a channel. The goal of the optimization is to maximise the farm’s energy extraction. The rectangular channel is 640 m x 320 m large. The farm area is in the channel center and 320 m x 160 m large.
- It shows how to:
set up a steady-state shallow water solver
add a tidal farm with 32 turbines;
define an optimisation objective, here the farm’s power production;
define an optimisation control, here the turbine positions;
define constraints to the controls: bounds to restrict the positions of the turbines to the farm bounds and minimum distance constraints between each turbine;
run the optimisation and retrieve the optimal turbine positions and farm power production.
Even though the domain in this demo is quite simple, the concept applies to more complex, realistic scenarios.
The farm layout optimisation is initialized with a regular layout of 32 turbines:

With this configuration, the flow speed with streamlines is:
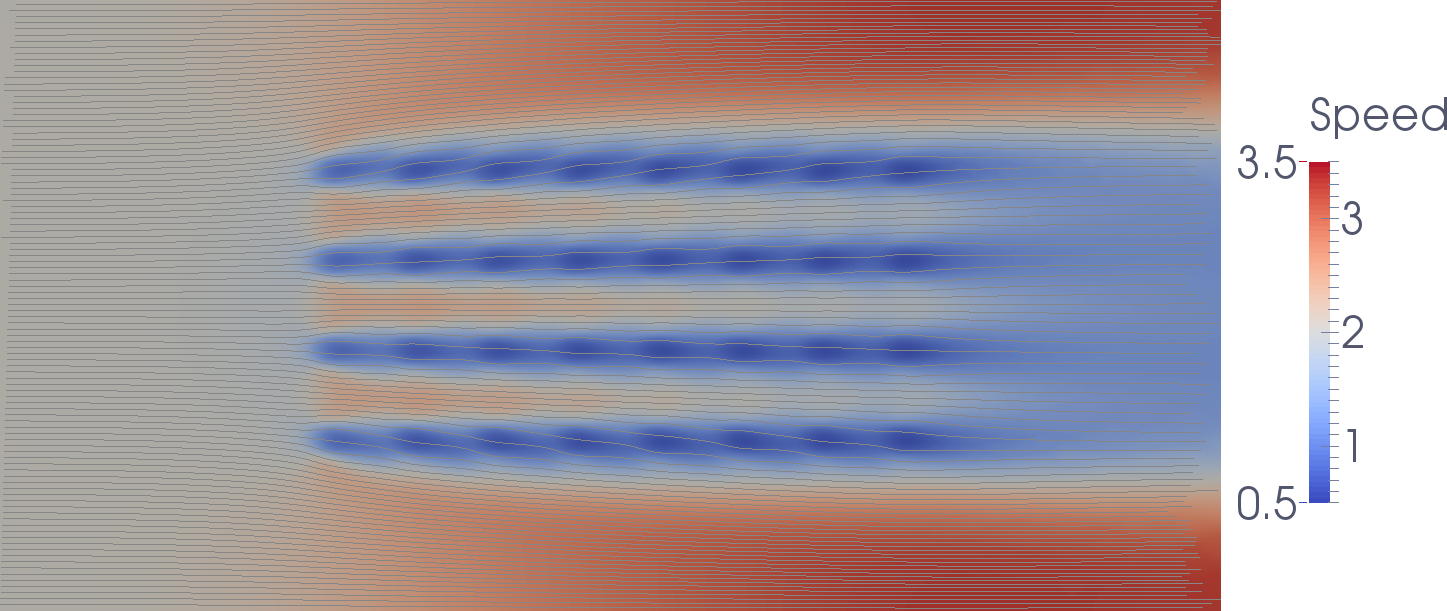
The power extraction by the farm (without taking losses into account) is 46 MW. This is 1.4 MW per turbine (32 turbines) which is unsatisfactory considering that placing a single turbine extracts 2.9 MW.
We can also try a staggered layout:

With this configuration, the flow speed with streamlines is:
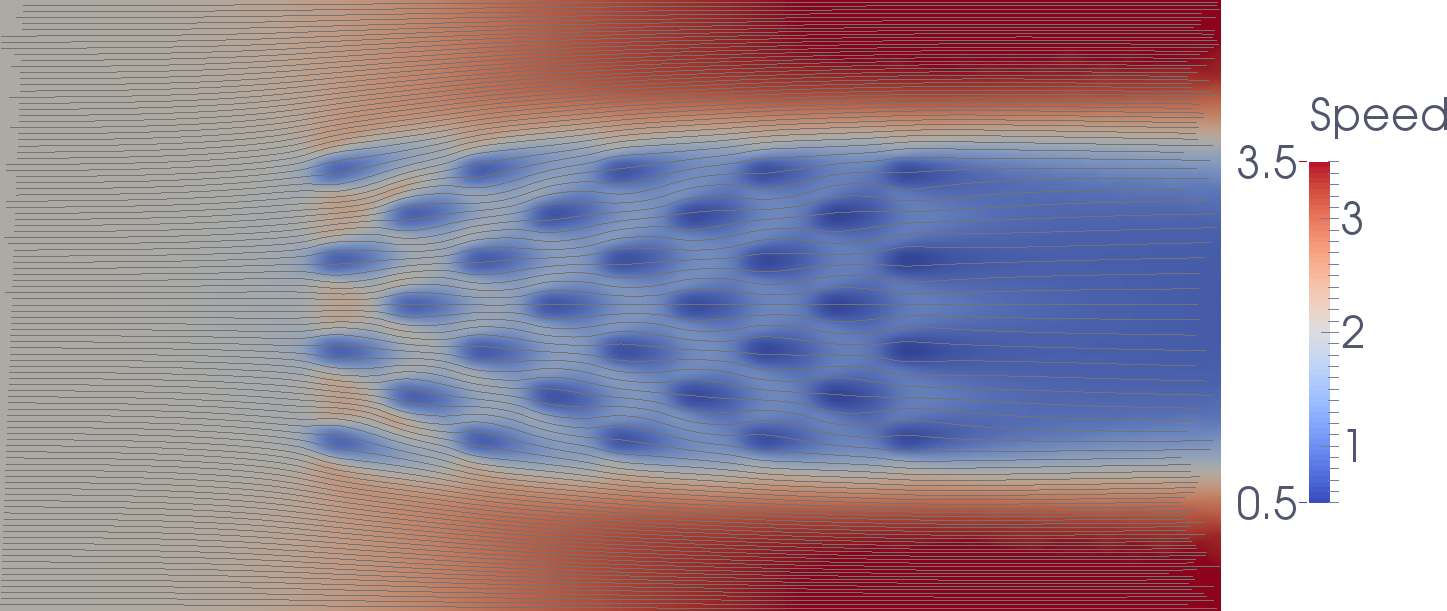
The power extraction by the farm (without taking losses into account) is 64 MW or 2.0 MW per turbine. Thats better but still non-optimal.
Applying the layout optimisation in OpenTidalFarm finishes after 92 iterations. The optimised farm layout is:

The optimization has arranged the turbines to “barrages” perpendicular to the flow. Furthermore, it added small north and east barrages of turbines that force the water to flow through the prependicular “barrages”. The associated flow speed with streamlines is:
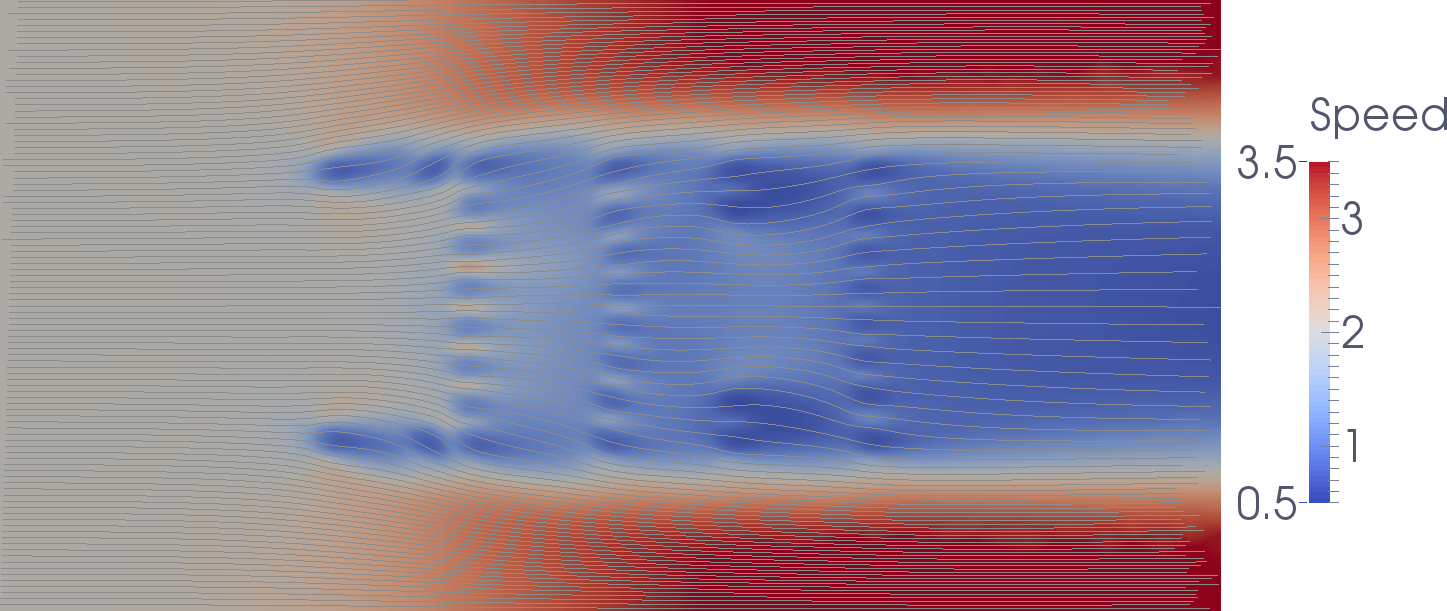
The power production of the optimised layout is 80 MW, or 2.5 MW per turbine. That is the optimisation increased the power production by 74 % compared to the initial layout!
5.1. Implementation¶
The first part of the program sets up a steady state shallow water problem, and is nearly identical to the Sinusoidal wave in a channel example:
from opentidalfarm import *
# Create a rectangular domain.
domain = FileDomain("mesh/mesh.xml")
# Specify boundary conditions.
bcs = BoundaryConditionSet()
bcs.add_bc("u", Constant((2, 0)), facet_id=1)
bcs.add_bc("eta", Constant(0), facet_id=2)
# The free-slip boundary conditions.
bcs.add_bc("u", facet_id=3, bctype="free_slip")
# Set the shallow water parameters
prob_params = SteadySWProblem.default_parameters()
prob_params.domain = domain
prob_params.bcs = bcs
prob_params.viscosity = Constant(2)
prob_params.depth = Constant(50)
prob_params.friction = Constant(0.0025)
The next step is to create the turbine farm. In this case, the farm consists of 32 turbines, initially deployed in a regular grid layout. This layout will be the starting guess for the optimization.
# Before adding turbines we must specify the type of turbines used in the array.
# Here we used the default BumpTurbine which defaults to being controlled by
# just position. The diameter and friction are set and a minimum distance
# between each turbine is specified. (if no minimum distance is set,
# it defaults to 1.5*diameter).
turbine = BumpTurbine(diameter=20.0, friction=12.0, minimum_distance=25.)
# A rectangular farm is defined using the domain and the site dimensions.
farm = RectangularFarm(domain, site_x_start=160, site_x_end=480,
site_y_start=80, site_y_end=240, turbine=turbine)
# Turbines are then added to the site in a regular grid layout.
farm.add_regular_turbine_layout(num_x=8, num_y=4)
prob_params.tidal_farm = farm
Now we can create the shallow water problem
problem = SteadySWProblem(prob_params)
Next we create a shallow water solver. Here we choose to solve the shallow water equations in its fully coupled form. We also set the dump period to 1 in order to save the results of each optimisation iteration to disk.
sol_params = CoupledSWSolver.default_parameters()
sol_params.dump_period = 1
solver = CoupledSWSolver(problem, sol_params)
Next we create a reduced functional, that is the functional considered as a pure function of the control by implicitly solving the shallow water equations. For that we need to specify the objective functional (the value that we want to optimize), the control (the variables that we want to change), and our shallow water solver.
functional = PowerFunctional(problem)
control = TurbineFarmControl(farm)
rf_params = ReducedFunctional.default_parameters()
rf_params.automatic_scaling = 5
rf = ReducedFunctional(functional, control, solver, rf_params)
As always, we can print all options of the ReducedFunctional with:
print rf_params
Now we can define the constraints for the controls and start the optimisation.
If no minimum distance constrained for the turbines is required, we can use the L-BFGS-B optimisation method:
lb, ub = farm.site_boundary_constraints()
f_opt = maximize(rf, bounds=[lb, ub], method="L-BFGS-B",
options={'maxiter': 100, 'ftol': 1e-06})
Otherwise, we need to create the minimum distance constraints and pass them to an optimisation method that supports such constraints (here we use SLSQP):
lb, ub = farm.site_boundary_constraints()
ieq = farm.minimum_distance_constraints()
f_opt = maximize(rf, bounds=[lb, ub], constraints=ieq, method="SLSQP",
options={'maxiter': 100, 'ftol': 1e-06})
5.2. How to run the example¶
The example code can be found in examples/channel-optimization/ in the
OpenTidalFarm source tree, and executed as follows:
$ python channel-optimization.py
You can speed up the calculation by using multiple cores (in this case 4) with:
$ mpirun -n 4 python channel-optimization.py
During the optimization run, OpenTidalFarm creates multiple files for inspection:
turbines.pvd: Stores the position and friction values of the turbines at each optimisation iteration.
iter_*: For each optimisation iteration X, the associated velocity and pressure solutions are stored in a directory named iter_X.
iterate.dat: A testfile that dumps the optimisation progress, e.g. number of iterations, function value, gradient norm, etc
The pvd files can be opened with the open-source software Paraview.