9. Resource assessment in the Orkney island¶
9.1. Introduction¶
This example demonstrates how OpenTidalFarm can be used for assessing the potential for tidal farms in a realistic domain. In particular, the task here is to identify the best locations to deploy tidal farms.
We will be simulating the tides in the Pentland Firth, Scotland for 6.25 hours, starting at 13:55 am on the 18.9.2001. To save computational time, we peform two steady-state solves for each simulation: one solve for times where the velocities reaches their peaks during one tidal cycle.
- This example uses the “continuous turbine approach”, as described in
Funke SW, Kramer SC, Piggott MD, Design optimisation and resource assessment for tidal-stream renewable energy farms using a new continuous turbine approach
To run this example, some data files must be downloaded separately by calling in the source code directory:
git submodule init
git submodule update
9.2. Implementation¶
We begin with importing the OpenTidalFarm module.
from opentidalfarm import *
from dolfin_adjoint import MinimizationProblem, TAOSolver, BaseRieszMap
We also need the datetime module for the tidal forcing.
import datetime
Next we define the UTM zone and band, as we we will need it multiple times later on.
utm_zone = 30
utm_band = 'V'
Next we create shallow water problem and attach the domain and boundary conditions
prob_params = MultiSteadySWProblem.default_parameters()
We load the mesh in UTM coordinates, and boundary ids from file
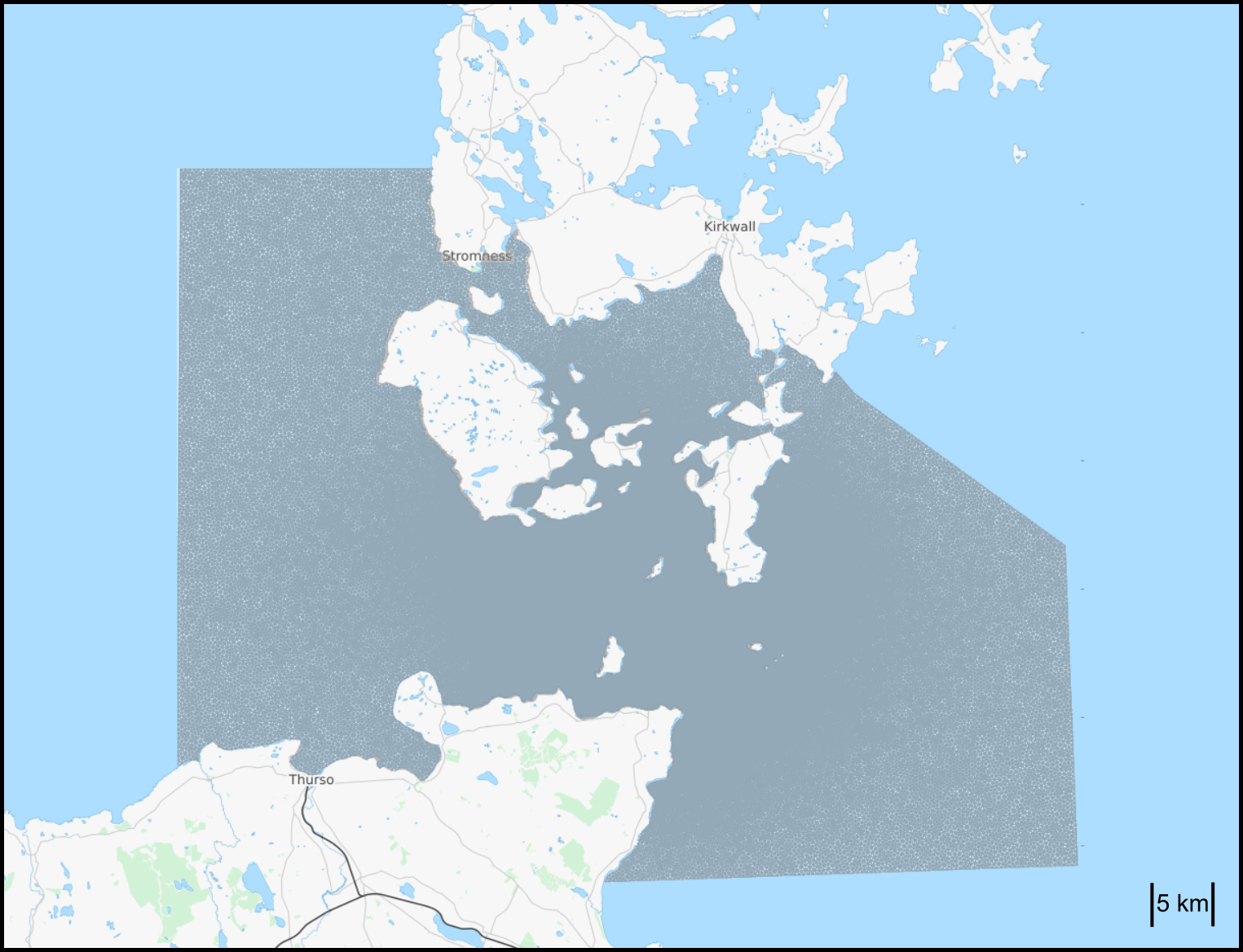
domain = FileDomain("../data/meshes/orkney/orkney_utm.xml")
prob_params.domain = domain
The mesh and boundary ids can be visualised with
plot(domain.facet_ids, interactive=True)
Next we specify boundary conditions. We apply tidal boundary forcing, by using
the TidalForcing class.
eta_expr = TidalForcing(grid_file_name='../data/netcdf/gridES2008.nc',
data_file_name='../data/netcdf/hf.ES2008.nc',
ranges=((-4.0,0.0), (58.0,61.0)),
utm_zone=utm_zone,
utm_band=utm_band,
initial_time=datetime.datetime(2001, 9, 18, 13, 55),
constituents=['Q1', 'O1', 'P1', 'K1', 'N2', 'M2', 'S2', 'K2'], degree=3)
bcs = BoundaryConditionSet()
bcs.add_bc("eta", eta_expr, facet_id=1)
bcs.add_bc("eta", eta_expr, facet_id=2)
The free-slip boundary conditions are a special case. The boundary condition type weak_dirichlet enforces the boundary value only in the normal direction of the boundary. Hence, a zero weak Dirichlet boundary condition gives us free-slip, while a zero strong_dirichlet boundary condition would give us no-slip.
bcs.add_bc("u", Constant((0, 0)), facet_id=3, bctype="strong_dirichlet")
prob_params.bcs = bcs
Next we load the bathymetry from the NetCDF file.
bathy_expr = BathymetryDepthExpression(filename='../data/netcdf/bathymetry.nc',
utm_zone=utm_zone, utm_band=utm_band, domain=domain.mesh, degree=3)
prob_params.depth = bathy_expr
Visualise it with
plot(prob_params.depth, mesh=domain.mesh, interactive=True)
The other parameters are set as usual.
Physical settings:
prob_params.viscosity = Constant(1e4)
prob_params.friction = Constant(0.0025)
Temporal settings:
prob_params.start_time = Constant(0)
prob_params.finish_time = Constant(6.25*60*60)
prob_params.dt = prob_params.finish_time
# The initial condition consists of three components: u_x, u_y and eta.
# Note that we set the velocity components to a small positive number, as some
# components of the Jacobian of the quadratic friction term is
# non-differentiable.
prob_params.initial_condition = Constant((DOLFIN_EPS, DOLFIN_EPS, 1))
We use the continuous turbine parametrisation by creating a SmearedTurbine object and pasing this to the Farm class. Note that we also specify the function space in which we want to have the continuous turbine farm represented - in this case piecewise constant functions.
turbine = SmearedTurbine()
W = FunctionSpace(domain.mesh, "CG", 1)
farm = Farm(domain, turbine, function_space=W)
prob_params.tidal_farm = farm
Next we define, which farms we want to optimize, by restricting the integral measure to the farm ids. The farm areas and their ids can be inspect with plot(farm.domain.cell_ids)
class Coast(SubDomain):
def inside(self, x, on_boundary):
return between(bathy_expr(*x), (25, 60))
coast = Coast()
farm_cf = CellFunction("size_t", domain.mesh)
farm_cf.set_all(0)
coast.mark(farm_cf, 1)
site_dx = Measure("dx")(subdomain_data=farm_cf)
farm.site_dx = site_dx(1)
Visualise it with
plot(farm_cf, interactive=True)
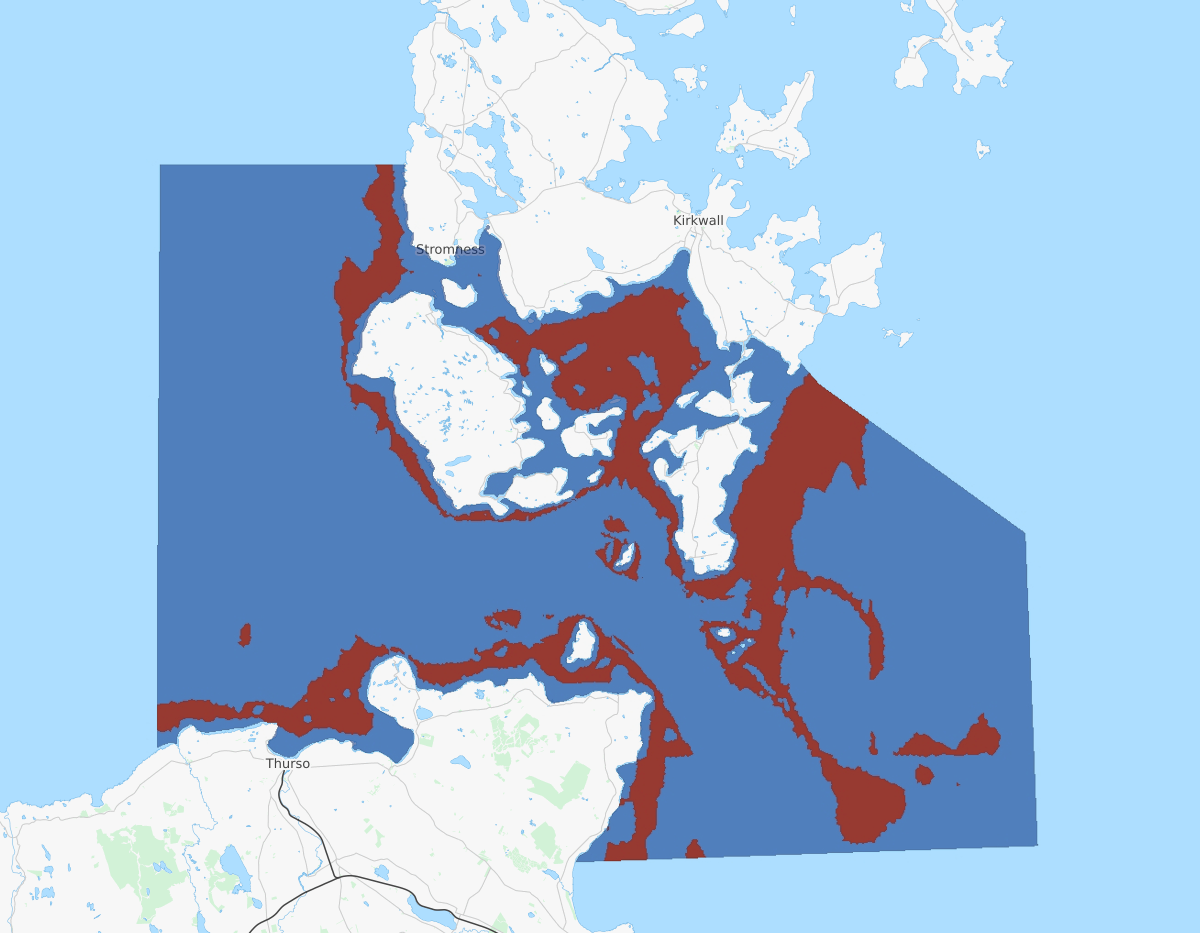
The red area marks the points that are suitable for turbine deployment.
Now we can create the shallow water problem
problem = MultiSteadySWProblem(prob_params)
Next we create a shallow water solver. Here we choose to solve the shallow water equations in its fully coupled form:
sol_params = CoupledSWSolver.default_parameters()
solver = CoupledSWSolver(problem, sol_params)
Now we can define the functional and control values:
functional = -PowerFunctional(problem)
# Optionally, add a cost term
# functional += alpha*CostFunctional(problem)
functional += 1e4*H01Regularisation(problem)
functional *= 1e-9 # Convert functional unit to GW
control = Control(farm.friction_function)
Only if using Optizelle: Optizelle is using an interiour point method, and hence we need to start at a feasible initial control (i.e. one that satisfies the bound constraints.
We create the reduced functional…
rf = FenicsReducedFunctional(functional, control, solver)
and run the simulation once with zero turbine friction to compute the base velocity:
rf([farm.friction_function])
The resulting velocities of the east-west tidal flow are:
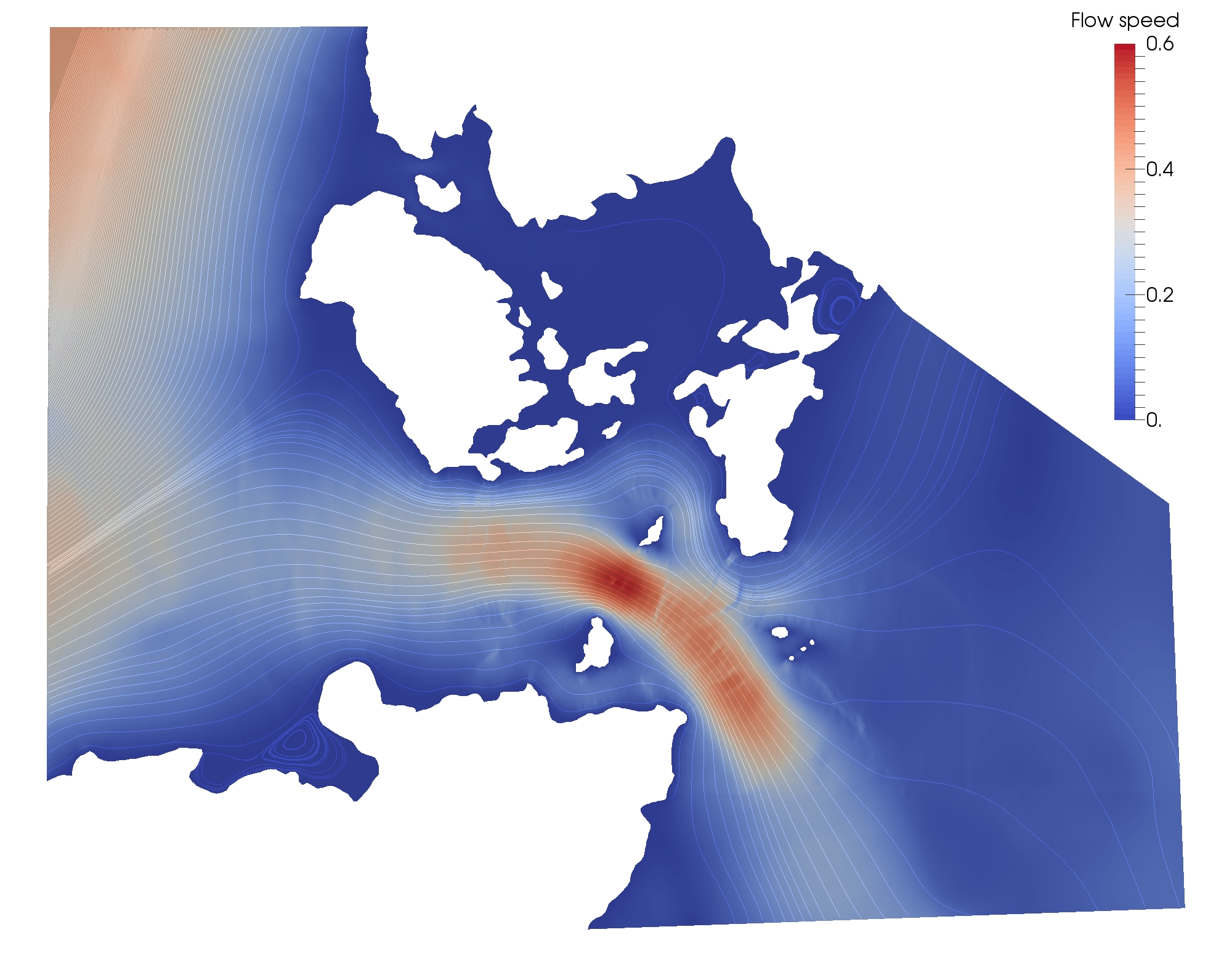
and of the west-east tidal flow:

# For the optimization, we use the more advanced TAO solver here,
# with a customized inner product to get better efficiency for non-uniform meshes.
farm_max = 10.0 # The maximum turbine density per area
opt_problem = MinimizationProblem(rf, bounds=(0.0, farm_max))
parameters = { "monitor": None,
"type": "blmvm",
"max_it": 50,
"subset_type": "matrixfree",
"fatol": 0.0,
"frtol": 1e-0,
"gatol": 0.0,
"grtol": 0.0,
}
# Define custom Riesz map
class L2Farm(BaseRieszMap):
def assemble(self):
u = TrialFunction(self.V)
v = TestFunction(self.V)
A = inner(u, v)*farm.site_dx
a = assemble(A, keep_diagonal=True)
a.ident_zeros()
return a
# Remove the riesz_map to switch from L2Farm norm to l2 norm
try:
opt_solver = TAOSolver(opt_problem, parameters, riesz_map=L2Farm(W))
f_opt = opt_solver.solve()
except:
# In case error occurs (typically because of an outdated PETSc or missing petsc4py), we fall back to scipy's L-BFGS-B method
f_opt = minimize(rf, bounds=(0.0, farm_max))
After 23 iterations (with the TAO solver), the optimisation terminates. We store the optimal turbine friction to file.
File("optimal_turbine.pvd") << f_opt
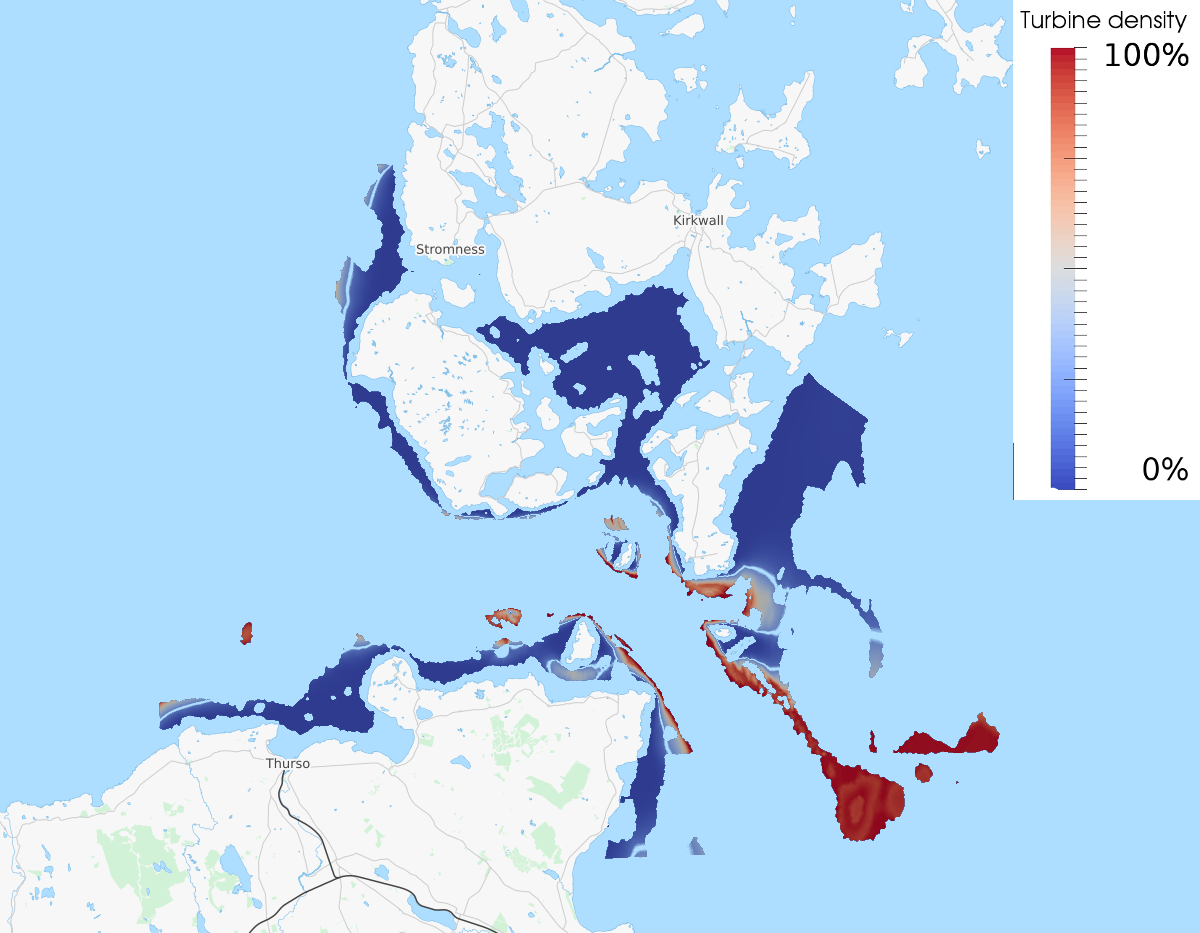
The code for this example can be found in examples/resource-assessment/ in the
OpenTidalFarm source tree, and executed as follows:
$ python compute_distance.py
$ mpirun -n 4 python resource-assessment.py